Lesson1: Describing the Orientation of a Spinning Top in 3D Space

Pre-Requisites: Knowledge of Dot and Cross Product

In order to understand the motion and physics of a spinning top, it is important to know how to describe the orientation of one at any given time.

For the purposes of our analysis, we will describe the orientation of a top with a point fixed at the origin using the following angles: roll, pitch and yaw.

1. Calculate Intermediate Pitch Vector (Figure 1)

The pitch of the top is the angle at which it leans toward the ground. Using the pitch angle we can calculate the x and y coordinate of its head using the following formula: 

x=rcosθ, y=rsinθ

where r is the top Height, and θ is the pitch angle

This formula comes from Trigonometric Projections. We can consider a unit circle with a given radius r.

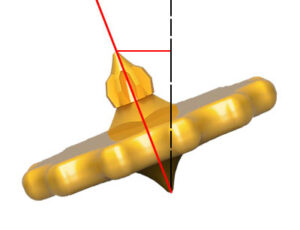
This formula describes the legs of a triangle that would be formed between the intersection of the radius, and circle edge as well as the points on the x and y axis that this intersection could be perpendicularly projected onto

2. Use Rotation Equations to Describe the Yaw

Once we have calculated this 2-dimensional intermediate vector, we can consider the rotation of this vector about the global Y-axis to be our Yaw.

Using Rodrigues’ Rotation Equations we can then determine the full coordinates to the head of the spinning top.

V’=vcosθ + (k×v)sinθ + k(k·v)(1−cosθ)

where v is our intermediate vector, k is the y axis, and θ is our given yaw

This equation describes 3 transformations that will happed to our intermediate vector:

1. The initial vector is scaled down proportionally to the cosine of the rotation angle: vcosθ
2. Then the vector is skewed in the new direction of rotation. (the direction of rotation is perpendicular as a result of using the cross product): (k×v)sinθ
3. Finally, the vector needs to be scaled back up to its original size, while maintaining its new direction: k(k·v)(1−cosθ)

3. Use Offset Pitch to describe the Edge of the Spinning Top

Finally we need to describe the rotation of our top using the roll angle. To demonstrate this, consider a given vector spanning from the origin to a point on the edge of the top at its widest point. 

Using the same method that was used to calculate the main axis of the top we can describe this vector, but with a greater pitch angle and a smaller height.

4. Describe the rotation of the top using the Roll Angle

Finally we can use the same rotation Equation as before to rotate this intermediate edge Vector about the main axis of the spinning top. This time using the roll angle for θ

Now that we can describe the state of a top at any given time, we can begin to observe how it changes over time as various forces act upon it.

Lesson 2 coming soon!

Interaction: Change the Roll, Pitch and Yaw to see how it affects the orientation of the top features.